LCA 与 RMQ 问题

LCA and RMQ

问题描述

LCA问题，即最近公共祖先问题。(Lowest common ancestor)

指在一个树或者有向无环图中同时拥有v和w作为后代的最深的节点。在这里，定义一个节点也是其自己的后代，因此如果v是w的后代，那么w就是v和w的最近公共祖先。

RMQ问题，即范围最值查询问题。(Range Minimum Query)

针对数据集的一种条件查询。若给定一个数组$A[1, n]$范围最值查询指定一个范围条件$i$到$j$，要求取出$A[i, j]$中最大/小的元素。

特别的，如果$A$上，任意两个相邻元素相差为$\pm1$，则称此$RMQ$问题为$\pm1RMQ$问题。

算法介绍

问题建模

LCA问题

对于一棵树而言，通过暴力的$DFS$计算总是可以求出一个可行的解出来。但是复杂度比较高，对于频繁的祖先查询很吃力。

这里介绍一种离线的查询方法，即在获得所有的询问情况以后，再进行查询的操作，这样可以按照树的$DFS$的顺序进行查找，方便快速给出答案。不难发现，“公共祖先”也是一种关系，可以想到使用并查集的方法进行维护。如果在进行$DFS$访问的时候，使用并查集维护一个祖先关系，就可以离线的给出最后的答案。具体的实现可以参考下面的$Tarjan$离线算法。

RMQ问题

对于另外一个问题，$RMQ$问题中，如果直接使用暴力的方法复杂度是$O(n^3)$，即对于$n^2$个区间，进行一次遍历操作，是不可以接受的。这里我们通常使用$Tarjan$的$Sparse-Table$算法，预处理时间是$O(n\lg n)$，但是查询时间只需要O(1)，而且常数很小。

我们使$d(i, j)$表示从$i$开始的，长度为$2^j$的一段元素中的最小值，则可以用递推的方法，进行计算$d(i, j)$：$d(i, j) = min { d(i, j - 1), d(i + 2^{j - 1}, j - 1) } $。

注意这里的$d$数组元素个数不超过$n\lg n$，每一项都可以在常数的时间内计算完毕，所以总的时间是$O(n\lg n)$。

查询操作就很简单了，我们令$k$为满足$2^k\leqslant R -L+1$的最大整数，则以$L$开头，$R$结尾的两个长度为$2^k$的区间合起来就可以覆盖查询区间$[L, R]$。

RMQ和LCA的转化

如果从一个更高的视角来看这个问题，其实$LCA$和$RMQ$之间存在着对应的关系，但是并不是那么明显。

$LCA$是在一棵树上找最近公共祖先，$RMQ$是在一个数组上找区间最值。$u, v$的最近公共祖先是$u$到$v$的简单路径经过节点中深度的最小值。通过$DFS$遍历，形成一个$DFS$序，这样处理得到的序列就可以作为一个$Path$数组，设$L_u$是$u$结点在$Path$中第一次出现的位置。那么$Path$从下标$L_u$到$L_v$经过的元素就是$u$到$v$的路径。在这个区间上查询深度最小的结点即可。

求解方法

LCA问题

正如前文提到的$Tarjan$算法，我们可以进行类似$DFS$的遍历，在遍历的过程中进行祖先的计算。

void LCA(int u) {
    ancestor[u] = u;
    for (u 的所有孩子节点 v) {
        LCA(v);
        setUnion(u, v);
        ancestor[setFind(u)] = u;
    }
    visited[u] = 1;
    for (和 u 有关的查询节点 v) {
        if (visited[v]) {
            find ancestor[setFind(v)]
        }
    }
}

如图，在$DFS$的遍历中，如果维护一个并查集，其中蓝色的部分为同一个祖先，紫色没有还没被更新完成。现在要查询黄色的节点，因为其没有子孙，所以直接进入查询过程，发现和图中蓝色的部分的公共祖先都是同样的（这张图里为其父节点）。所以可以直接给出正确的答案。但是如果查询其他没有加入并查集的节点，只能进行反向查询（比如$(u,v)$需要在$(v, u)$处查询），所以问题必须要正反向加入两次，最后一定可以给出答案。

RMQ问题

$RMQ$算法实现十分的简单，其代码也很短，这里直接给出代码：

void RMQ_init (vector<int> &A) {	// RMQ建表
  	int n = A.size();
  	for (int i = 0; i < n; ++i)
      	d[i][0] = A[i];
  	for (int j = 1; (1 << j) <= n; ++j)
      	for (int i = 0; i + (1 << j) - 1 < n; ++i)
          	d[i][j] = min(d[i][j - 1], d[i + (1 << (j - 1))][j - 1]);
}

int RMQ (int L, int R) {	// 查询
  	int k = 0;
  	while ((1 << (k + 1)) <= R - L + 1)	++k;
  	return min(d[L][K], d[R - (1 << k) + 1][k]);
}

解题报告

Poj 1470 Closest Common Ancestors

问题描述

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

• Input

  The data set, which is read from a the std input, starts with the tree description, in the form:

  nr_of_vertices
  vertex:(nr_of_successors) successor1 successor2 … successorn
  …
  where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
  nr_of_pairs
  (u v) (x y) …

  The input file contents several data sets (at least one).
  Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

• Output

  For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
  For example, for the following tree: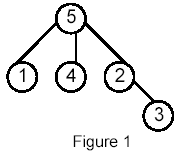

  

算法设计

此题比较简单，基本就是$LCA$算法的简单应用。因为是离线算法，所以我们需要将询问的进行储存，最后一并输出。

程序代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int MAXN = 1000 + 10;
int father[MAXN];
int Rank[MAXN];
int visited[MAXN];
int ancestor[MAXN];
int res[MAXN];
vector<int> son[MAXN];
vector<int> q[MAXN];
int n;

int setFind(int u) {
    if (father[u] == u)
        return u;
    father[u] = setFind(father[u]);
    return father[u];
}
void setUnion(int u, int v) {
    u = setFind(u);
    v = setFind(v);
    if (u == v)
        return;
    if (Rank[v] > Rank[u]) {
        father[u] = v;
        Rank[v] += Rank[u];
    }
    else {
        father[v] = u;
        Rank[u] += Rank[v];
    }
}
void LCA(int u) {
    ancestor[u] = u;
    for (vector<int>::iterator v = son[u].begin(); v != son[u].end(); ++v) {
        LCA(*v);
        setUnion(u, *v);
        ancestor[setFind(u)] = u;
    }
    visited[u] = 1;
    for (vector<int>::iterator v = q[u].begin(); v != q[u].end(); ++v) {
        if (visited[*v]) {
            ++res[ancestor[setFind(*v)]];
        }
    }
}
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    while (scanf("%d", &n) == 1) {
        int u, v;
        int i;
        for (i = 1; i <= n; ++i) {
            father[i] = i;
            son[i].clear();
            q[i].clear();
        }
        memset(Rank, 1, sizeof(Rank));
        memset(visited, 0, sizeof(visited));
        memset(ancestor, 0, sizeof(ancestor));
        memset(res, 0, sizeof(res));
        for (i = 1; i <= n; ++i) {
            int sonCnt;
            scanf("%d:(%d)", &u, &sonCnt);
            while(sonCnt--) {
                scanf("%d", &v);
                ++res[v];
                son[u].push_back(v);
            }
        }
        int qCnt;
        scanf("%d", &qCnt);
        while(qCnt--) {
            scanf(" (%d %d)", &u, &v);
            q[u].push_back(v);
            q[v].push_back(u);
        }
        for (i = 1; i <= n; ++i) {
            if (!res[i])
                break;
        }
        memset(res, 0, sizeof(res));
        LCA(i);
        for (i = 1; i <= n; ++i) {
            if (res[i])
                printf("%d:%d\n", i, res[i]);
        }
    }
}

性能分析

题目基本是裸的$LCA$最后的复杂度是$O(n + q)$。

编程技术技巧

此题基本没有太多技巧，唯一需要注意的是找到祖先以后，需要将数据保存下来，最后一并输出。

Poj 1986 Distance Queries

问题描述

Farmer John’s cows refused to run in his marathon since he chose a path much too long for their leisurely lifestyle. He therefore wants to find a path of a more reasonable length. The input to this problem consists of the same input as in “Navigation Nightmare”,followed by a line containing a single integer K, followed by K “distance queries”. Each distance query is a line of input containing two integers, giving the numbers of two farms between which FJ is interested in computing distance (measured in the length of the roads along the path between the two farms). Please answer FJ’s distance queries as quickly as possible!

• Input

  Lines 1..1+M: Same format as “Navigation Nightmare”

  Line 2+M: A single integer, K. 1 <= K <= 10,000

  Lines 3+M..2+M+K: Each line corresponds to a distance query and contains the indices of two farms.

• Output

  Lines 1..K: For each distance query, output on a single line an integer giving the appropriate distance.

算法设计

题目也比较简单，基本可以看作是普通的$LCA$问题的求解，但是需要注意的是，我们需要求出两个点的路径长度，这里还是运用了求和的思想。通过一次$DFS$的遍历，指定编号的同时，记录每个点到根节点的距离。这样，如果需要计算$i$和$j$点的距离，我们只需要通过$distance(i) + distance(j) - 2 * distance(ancestor(i, j))$来进行计算。

程序代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
struct Edge {
    int v;
    int d;
    Edge(int v, int d): v(v), d(d) {}
};
struct Question {
    int v;
    int time;
    Question(int v, int t): v(v), time(t) {}
};
const int MAXN = 40000 + 10;
int father[MAXN];
int Rank[MAXN];
int visited[MAXN];
int ancestor[MAXN];
int firstFind[MAXN];
vector<Edge> son[MAXN];
vector<Question> q[MAXN];
int Distance[MAXN];
int res[MAXN];
int n, m, u, v, d, i;

int setFind(int u) {
    if (father[u] == u)
        return u;
    father[u] = setFind(father[u]);
    return father[u];
}
void setUnion(int u, int v) {
    u = setFind(u);
    v = setFind(v);
    if (u == v)
        return;
    if (Rank[v] > Rank[u]) {
        father[u] = v;
        Rank[v] += Rank[u];
    }
    else {
        father[v] = u;
        Rank[u] += Rank[v];
    }
}
void LCA(int u, int sumDistance) {
    ancestor[u] = u;
    Distance[u] = sumDistance;
    firstFind[u] = 1;
    for (vector<Edge>::iterator v = son[u].begin(); v != son[u].end(); ++v) {
        if (firstFind[v->v])
            continue;
        LCA(v->v, v->d + sumDistance);
        setUnion(u, v->v);
        ancestor[setFind(u)] = u;
    }
    visited[u] = 1;
    for (vector<Question>::iterator v = q[u].begin(); v != q[u].end(); ++v) {
        if (visited[v->v]) {
            res[v->time] = Distance[u] + Distance[v->v] - 
                            (Distance[ancestor[setFind(v->v)]] << 1);
        }
    }
}

int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    while (scanf("%d %d", &n, &m) == 2) {
        for (i = 1; i <= n; ++i) {
            father[i] = i;
            son[i].clear();
            q[i].clear();
        }
        memset(Rank, 1, sizeof(int) * n + 1);
        memset(visited, false, sizeof(int) * n + 1);
        memset(firstFind, 0, sizeof(int) * n + 1);
        char tmp[10];
        while (m--) {
            scanf("%d %d %d %s", &u, &v, &d, tmp);
            son[u].push_back(Edge(v, d));
            son[v].push_back(Edge(u, d));
        }
        scanf("%d", &m);
        for (i = 0; i < m; ++i) {
            scanf("%d %d", &u, &v);
            q[u].push_back(Question(v, i));
            q[v].push_back(Question(u, i));
        }
        LCA(1, 0);
        for (i = 0; i < m; ++i) {
            printf("%d\n", res[i]);
        }
    }
}

性能分析

此题和上一道题目区别不是很大，主要是需要事先计算开始的$DFS$序列，花费时间是$O(n)$。所以基本的复杂度和$LCA$一致，为$O(n\lg n)$。

编程技术技巧

此题比较直接，和在树状数组里遇到的题目基本一致，没有太多的技巧可以介绍。

Poj 2763 Housewife Wind

问题描述

After their royal wedding, Jiajia and Wind hid away in XX Village, to enjoy their ordinary happy life. People in XX Village lived in beautiful huts. There are some pairs of huts connected by bidirectional roads. We say that huts in the same pair directly connected. XX Village is so special that we can reach any other huts starting from an arbitrary hut. If each road cannot be walked along twice, then the route between every pair is unique.

Since Jiajia earned enough money, Wind became a housewife. Their children loved to go to other kids, then make a simple call to Wind: ‘Mummy, take me home!’

At different times, the time needed to walk along a road may be different. For example, Wind takes 5 minutes on a road normally, but may take 10 minutes if there is a lovely little dog to play with, or take 3 minutes if there is some unknown strange smell surrounding the road.

Wind loves her children, so she would like to tell her children the exact time she will spend on the roads. Can you help her?

• Input

  The first line contains three integers n, q, s. There are n huts in XX Village, q messages to process, and Wind is currently in hut s. n < 100001 , q < 100001.

  The following n-1 lines each contains three integers a, b and w. That means there is a road directly connecting hut a and b, time required is w. 1<=w<= 10000.

  The following q lines each is one of the following two types:

  Message A: 0 u
  A kid in hut u calls Wind. She should go to hut u from her current position.
  Message B: 1 i w
  The time required for i-th road is changed to w. Note that the time change will not happen when Wind is on her way. The changed can only happen when Wind is staying somewhere, waiting to take the next kid.

• Output

  For each message A, print an integer X, the time required to take the next child.

算法设计

此题算法设计很复杂，恰好用到了前文提出的各个要点，在这里使用$ST$算法进行计算，通过$DFS$序转化，最后用$LCA$转$RMQ$进行查询。和上一题一样，仍然需要使用$distance(i) + distance(j) - 2 * distance(ancestor(i, j))$的思想进行处理，但是因为母亲的位置是移动的，如果使用在线算法，对于这道题目来说会比较方便。所以需要使用一个树状数组，进行$O(\lg n)$的求和操作。

程序代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int MAXN = 100000 + 10;
int BIT[MAXN << 1];
inline int lowbit(int x) {
    return x & (-x);
}
inline int sum(int x) {
    int res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}
inline void edit(int x, int delta) {
    while (x < (MAXN << 1)) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}

struct Edge {
    int to;
    int next;
};
Edge edge[MAXN * 2];
int edgeWeight[MAXN];
int head[MAXN];
int cntEdge;
inline void addEdge(int u, int v) {
    edge[++cntEdge].to = v;
    edge[cntEdge].next = head[u];
    head[u] = cntEdge;
}

int id[MAXN * 2], idToPoint[MAXN * 2];
int depth[MAXN * 2];
int cnt;
int in[MAXN], out[MAXN];
void dfs(int u, int d, int father) {
    id[u] = ++cnt;
    idToPoint[cnt] = u;
    depth[cnt] = d;
    for (int i = head[u]; i != 0; i = edge[i].next) {
        if (edge[i].to == father)
            continue;
        int edgeId = (i + 1) >> 1;
        edit(cnt + 1, edgeWeight[edgeId]);
        in[edgeId] = cnt + 1;
        dfs(edge[i].to, d + 1, u);
        idToPoint[++cnt] = u;
        edit(cnt, -edgeWeight[edgeId]);
        out[edgeId] = cnt;
        depth[cnt] = d;
    }
}

int dp[MAXN * 2][20];
int cmp(int x, int y) {
    return depth[x] < depth[y];
}
void ST(int n) {
    for (int i = 1; i <= n; ++i) {
        dp[i][0] = i;
    }
    int len = (int)(log(n * 1.0) / log(2.0));
    for (int j = 1; j <= len; ++j) {
        for (int i = 1; i <= n; ++i) {
            if (i + (1 << j) - 1 > n)
                break;
            dp[i][j] = min(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1], cmp);
        }
    }
}
int RMQ(int x, int y) {
    if (x > y)
        swap(x, y);
    int k = (int)(log(y - x + 1.0) / log(2.0));
    return min(dp[x][k], dp[y + 1 - (1 << k)][k], cmp);
}

int LCA(int u, int v) {
    return idToPoint[RMQ(id[u], id[v])];
}

int n, mother, state, childCall, num, delta, qtimes;
int u, v;
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    while(scanf("%d %d %d", &n, &qtimes, &mother) == 3) {
        memset(dp, 0, sizeof(dp));
        memset(BIT, 0, sizeof(BIT));
        memset(head, 0, sizeof(head));
        cnt = 0;
        cntEdge = 0;
        for (int i = 1; i <= n - 1; ++i) {
            scanf("%d %d %d", &u, &v, edgeWeight + i);
            addEdge(u, v);
            addEdge(v, u);
        }
        dfs(1, 1, -1);
        ST((n << 1) - 1);
        while(qtimes--) {
            scanf("%d", &state);
            if (state) {
                scanf("%d %d", &num, &delta);
                edit(in[num], delta - edgeWeight[num]);
                edit(out[num], edgeWeight[num] - delta);
                edgeWeight[num] = delta;
            }
            else {
                scanf("%d", &childCall);
                int root = LCA(mother, childCall);
                printf("%d\n", sum(id[mother]) + sum(id[childCall]) - (sum(id[root]) << 1));
                mother = childCall;
            }
        }
    }
}

性能分析

通过$DFS$将$LCA$问题转化为$RMQ$问题是$O(n)$级别的算法，对于$RMQ$本身来说，需要进行$O(n\lg n)$的时间进行建表的操作，树状数组的查询也是$O(\lg n)$级别的，所以考虑有$n$次的查询，总体的复杂度是$O(n\lg n)$。

编程技术技巧

题目本身比较复杂，融合的内容比较多，需要对于修改-查询这一类的算法都比较清楚熟练，才能比较好的完成此题。